Манипуляция статистикой
 | Незавершённая статья Эта статья находится в процессе написания. Сюда следует добавить недостающий материал и устранить проблемы в оформлении и содержании. Вы можете помочь в доработке статьи. Добавьте сюда больше информации. |
Как говорят, «есть ложь, есть наглая ложь, и есть статистика». А почему? А потому что статистикой часто манипулируют, чтобы ложные данные выглядели наукообразно и правдоподобно.
Применительно к политической жизни манипуляция статистикой важна на выборах. Можно сымитировать всестороннюю поддержку кандидата и шаткое преимущество превратить в уверенное. А можно посеять зёрна сомнения насчёт честности выборов.
- Если не показан источник данных — они искусственные.
Манипуляция источниками данных
Нерепрезентативная выборка
Есть два нарекания к плохим выборкам: маленькая (слишком большие погрешности) и с перекосами (не отражает структуры всей генеральной совокупности).
Собрать достаточно репрезентативную выборку — это в своём роде искусство, и если оно не прокатывает, может случиться забавное.
Из книги Дарелла Хаффа «Как лгать при помощи статистики». Журнал Literary Digest по результатам широчайших (10 млн) опросов пришёл к выводу, что на выборах победит Альфред Лэндон. А победил Франклин Рузвельт. Просто те, кто имели телефон и подписывались на Literary Digest, были достаточно богаты и поддерживали Республиканскую партию.
Другой пример оттуда же. Для испытания прививки от полиомиелита 450 детей привили, 680 оставили. Во время эпидемии ни один привитый не заболел. Здесь вопрос в крайней редкости болезни, в группе такой численности заболеют в среднем двое, и чтобы результат был статистически значим, нужна выборка раз в пятнадцать больше.
Разновидность: ошибка выжившего
Один из важнейших способов получить выборку с перекосами так, чтобы никто ничего не заподозрил. Когда есть «выжившие», по которым информация легкодоступна, и «погибшие», по которым информации нет, заманчиво взять выборку из «выживших» и сказать: вот репрезентативная выборка. Но это неверно: важная информация скрывается среди «погибших», и хотелось бы восстановить, какая именно. Особенно если задача — не стать «погибшим».
Начнём с примера, который ввёл в обиход математиков ошибку выжившего. Абрахам Вальд, работая математиком на силы Коалиции во Второй мировой войне, получил задачу. Не все бомбардировщики возвращались с полётов. Те, которые всё-таки вернулись, оказались изрешечены пробоинами. Все пробоины нанесли на одну модель; крылья и хвост оказались все в пробоинах, а кабина и центроплан — чистые. Верно ли, что надо добавить брони на крылья и хвост? Вальд сказал: нет! Они все в пробоинах, потому что достаточно прочны. Самолёт, которому попали в кабину, не вернётся, которому попали в крыло — долетит. Потому укреплять надо как раз чистые зоны.
Точно так же из старых машин и зданий дошли наиболее прочные и практичные, рекламист Гельмут Крон («Фольксваген») сыграл на этом: «Теперь таких не делают».
«Погибших» можно делать и искусственно, этим грешат реалити-шоу, которые выводят наименее перспективных участников, пока те не заполучили своих поклонников.
Разновидность: ущербная процедура сбора
Когда сервис «Пробок нет» обратился к ГИБДД Москвы насчёт вторичных ДТП со смертельным исходом (ДТП с автомобилями, стоящими в ДТП), они насчитали 8 штук. В том ДТП, где автобус въехал в ДТП и люди чудом остались живы, в карточке стояло: «2 участника». Отсмотрев множество видео, они обнаружили ещё 25 таких ДТП с 29 погибшими (Москва, один год).
Взять только те данные, которые подтверждают точку зрения (метод техасского стрелка)
Метод техасского стрелка: стрельнуть и нарисовать мишень там, куда стрельнул, а неудачные пробоины залатать. Это связано с другим методом демагогии: Свиногогия.
Из книги Дарелла Хаффа «Как лгать при помощи статистики»: «Предположим, некая немногочисленная группа потребителей в течение полугода ведет учет состояния своих зубов, а потом переключается на пасту от Doakes. Далее можно ожидать одного из трех вариантов: кариеса станет больше, кариеса станет ощутимо меньше или никаких изменений не последует. Если события пойдут по первому или последнему варианту, производитель пасты просто зафиксирует эти показатели (где-нибудь у себя, вдали от глаз общественности) и предпримет новые попытки. Рано или поздно в дело вмешается случай, и у испытуемых зафиксируют-таки значительное улучшение, достойное газетных заголовков, а то и целой рекламной кампании. И случится это независимо от того, пользуются ли испытуемые пастой Doakes, питьевой содой или своим привычным средством по уходу за зубами».
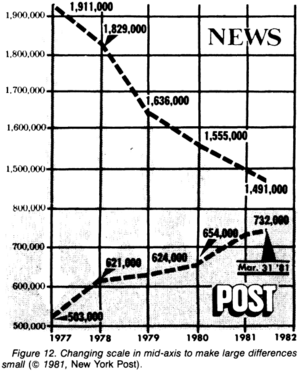
Графики, сделанные по методу техасского стрелка, часто отличаются необоснованно рваным масштабом по оси X.
Давать на сравнение совершенно разные цифры
Известный рекламный трюк: подключить второй фактор и сделать вид, что он ни к чему. Из статьи Сергея Абдульманова «Как айтишник по магазинам ходил»:
А вот про такое я даже не думал. Давайте ещё раз: они обещают мне заметный результат через две недели. Как они проверили? Мыли голову вот этой штукой и, внимание, фокус, ещё одной другой штукой. И эти обе штуки вместе оказали заметный результат. Почти идеальная логика.
Из книги Дарелла Хаффа «Как лгать при помощи статистики»:
В Америке псевдообоснованные цифры переживают бум раз в четыре года. Впрочем, это не свидетельствует о циклической природе таких цифр, а просто напоминает, что именно с такой периодичностью проходят выборы. Предвыборное заявление, обнародованное Республиканской партией в октябре 1948 г., целиком и полностью построено на цифрах. Создается видимость, что эти цифры связаны друг с другом, но это не так:
Когда Дьюи в 1942 г. был избран на пост губернатора, минимальный размер зарплаты учителей в некоторых районах составлял такую малость, как $900 в год. Сегодня школьные учителя в штате Нью-Йорк получают самые высокие зарплаты в мире. По рекомендации губернатора Дьюи, которая основывалась на сведениях, полученных в ходе работы назначенного им комитета, легислатура штата выделила из бюджета штата $32 000 000 на обеспечение немедленного повышения заработной платы школьным учителям. В результате минимальный размер зарплаты учителя в Нью-Йорке варьируется в пределах от $2500 до $5325.
Совершенно не исключено, что мистер Дьюи проявил себя как друг учителей, да только приведенные цифры об этом не свидетельствуют. Это старый как мир трюк с «было» и «стало», когда для показа разительных перемен втихомолку приводят в действие ряд факторов, а потом представляют дело так, будто эти факторы ни при чем. Здесь у нас имеется «было» $900 и «стало» от $2500 до $5325. Это, бесспорно, создает впечатление, что положение улучшилось. Но меньшая цифра отражает нижний порог зарплаты учителя в каком-нибудь сельском районе штата, а цифры побольше — диапазон заработных плат учителей в самом Нью-Йорке. Может быть, при губернаторе Дьюи улучшения действительно произошли, а может быть, и нет.
Оттуда же:
Ещё один образчик подмены объекта исследования явил сенатор Уильям Лангер, когда возопил, что «мы могли бы взять заключенного из „Алькатраса“ и поместить на содержание в „Уолдорф-Асторию“ — дешевле бы обошлось…» Дело в том, что сенатор от Северной Дакоты ссылался на ранее опубликованные данные, что содержать узника в тюрьме «Алькатрас» стоит $8 в сутки, а «это стоимость номера в хорошем сан-францисском отеле». Здесь произошла подмена общих затрат на содержание (в «Алькатрасе») на одну только стоимость номера в отеле.
Подмена источника данных
Как говорят, «по результатам опроса, проведённого в Интернете, 100 % населения подключены к интернету».
Более тонкая манипуляция: скажи возраст жены. На 35 годах будет пик, выше, чем 34 или 36 — просто потому, что если кто-то возраст не помнит, даёт округлённую цифру. Куда надёжнее спрашивать год рождения жены.
Манипуляция обработкой
Спутать среднее, медиану, моду и квантиль достаточного уровня
Начнём с неформальных определений.
- Математическое ожидание случайной величины — это, грубо говоря, «среднее по бесконечной выборке».
- Матожидание имеет смысл, когда данные разных испытаний каким-то образом суммируются: если в столовой средний чек 120 тугриков, то, обслужив 15 человек, официант принесёт около 1800 тугриков выручки.
- Мода — наиболее часто встречающееся значение.
- Квантиль уровня α — такой x, что вероятность попасть в диапазон (−∞; x) будет α, а в диапазон [x; +∞) — соотвественно, 1−α. Слово «квантиль» мужского рода.
- Квантиль уровня 0,5 — вероятность «недолёта» 0,5 и вероятность «перелёта» 0,5 — называется медианой.
- Три квантиля уровней 0,25, 0,5 и 0,75 — квартили. Девять квантилей уровней с 0,1 по 0,9 — децили. 99 квантилей с 0,01 по 0,99 — процентили.
- Квантили важны, если испытание однократно и надо рассчитать вероятность попасть в диапазон. Квантили робастны (большие выбросы в данных не утащат квантиль далеко), и потому лучше среднего отражают порядок цифр: например, при медиане в 30 тыс. тугриков разнорабочему вряд ли стоит рассчитывать больше, чем на 15.
У нас в статистике, к сожалению, нет математически заданной случайной величины, есть только выборки. Что с ними можно сделать?
- Математическое ожидание можно приблизить выборочным средним.
- Чтобы найти моду, строят гистограмму, сглаживают её, убирая случайные колебания, и её максимум будет модой. Несколько максимумов — несколько мод.
- Чтобы найти медиану, выстраивают экспериментальные значения по порядку и берут центральное. Точно так же — при достаточном размере выборки — можно получить любой квантиль.
Когда распределение симметричное и колоколообразное, матожидание, медиана и мода совпадают. Но часто статистика имеет дело с несимметричными распределениями. Так, если в фирме босс, получающий 10000 $, два инженера с доходом 1500, пять токарей с доходом 800 и семь грузчиков с доходом 300, имеем среднее 1273 $, медиану 800 и моду 300. Выбирай любое среднее в зависимости от того, в каком свете хочешь показать доходы.
Другое заблуждение более хитрое — и, к сожалению, очень распространённое. Берём медиану или среднее, и считаем, что эта цифра — надёжная граница. Живой пример.
Не все из нас живут под метро, а автобусы обычно ходят случайно и с неприемлемо долгими интервалами. Допустим, поездка «в среднем» длится 45 минут. Подсознательно хочется выходить за 45 минут до времени Ч, особенно сильным мужчинам, которые могут бегом подсократить пешеходное плечо. Но слишком уж часто приходится бежать: если ваше «среднее» — это медиана, в половине случаев вы будете опаздывать; если это среднее арифметическое — несколько реже. Успевать при любых обстоятельствах? Закладываться на такие редкие события, как две аварии подряд, растянувшие пробку на всю улицу, выгодно только там, где опоздание дорого стоит: съёмки/соревнования/смотры (профессионалам за них щедро платят, а у любителей бывают лишь пару раз в год), самолёт… Потому надо говорить: нас, например, устраивает успевать на 90 % встреч. Другими словами, нужный срок выхода — квантиль уровня 0,9.
Из книга Дарелла Хаффа «Как лгать при помощи статистики»: «Сходным образом мелкие опущенные детали в труде под названием „Нормы развития Гезелла“ ввергли в панику папочек и мамочек. Дай только родителю прочитать раздел, где говорится, что в возрасте стольких-то месяцев ребенку уже полагается сидеть, и он сейчас же примерит это к собственному малышу. А поскольку примерно половина детей к указанному возрасту всё ещё не научилась сидеть, это сделало несчастными многих и многих родителей. Этого недоразумения во многом удалось бы избежать, если бы наряду с показателем „нормы“ или среднего значения был бы указан диапазон этой самой нормы. Тогда родители увидели бы, что их дети попадают в пределы нормы и прекратили бы беспокоиться по поводу мелких и ничего не значащих отклонений».
Спутать априорную, условную и апостериорную вероятность
Допустим, мы исследуем вероятность заболеть, если был привит и если не был. Тогда у нас:
- Априорная вероятность — вероятность заболеть (уколот ли — неизвестно).
- Условная вероятность — вероятность заболеть, если был привит. Или если не был.
- Апостериорная вероятность — вероятность, что ты привит, если ты заболел (или если не заболел).
Априорная вероятность связана с условными по формуле полной вероятности. Апостериорная вероятность связана с условными по формуле Байеса.
Например (цифры выдуманные): из 100 уколотых заболели 20. Из 10 отказавшихся заболели все. Тогда:
- Априорная вероятность — 30/110 ≈ 0,27.
- Условная вероятность, если привит — 0,2. Условная вероятность, если не привит — 1.
- Апостериорная вероятность быть привитым, если не заболел — 1. Если заболел — 20/30 ≈ 0,67.
Вот мы смотрим на последнюю цифру и говорим: двое из трёх заболевших привиты! А ведь прививка превращает почти верную болезнь в 20 %!
Из книги Дарелла Хаффа «Как лгать при помощи статистики»: «Уровень смертности в военно-морском флоте США в период Испано-Американской войны 1898 г. составлял девять человек на тысячу. За тот же период уровень смертности среди гражданского населения Нью-Йорка достигал шестнадцати человек на тысячу. Позже эти цифры использовали вербовщики, чтобы показать: служить в ВМС безопаснее, чем находиться за его пределами. Допустим, что сами эти цифры точны (вероятно, так оно и есть). Давайте остановимся на мгновение и проверим, сообразите ли вы, что лишает практически всякого смысла сами эти цифры, или хотя бы заключение, которое выводили из них вербовщики. Всё дело в том, что группы, к которым относятся вышеуказанные цифры, несопоставимы. В рядах ВМС служат главным образом молодые мужчины, признанные здоровыми. Гражданское же население состоит среди прочего из малых детей, стариков и больных, и для этих категорий населения уровень смертности выше, где бы они ни находились».
На языке математики: априорную вероятность (вероятность умереть на гражданке, независимо от того, годен ли ты в армию) выдаём за условную (вероятность умереть на гражданке, если ты годен).
Если одна из вероятностей мала, полученные цифры сильно отличаются от интуитивных. Например: алкотестер одного трезвого из ста принимает за пьяного (а вот пьяного обнаружит всегда). На дороге один пьяный на тысячу трезвых. В таком случае лишь 9 % попавшихся действительно пьяны. Этим осложняется борьба с терроризмом: когда по городу-миллионнику ходят сто террористов, какие нужны вероятности, чтобы не ломать жизни невинным! (rwp:Ошибка базового процента)
Фриц Морген задал очень милую задачу про апостериорную вероятность, вот ответ на неё.
Существует математический анекдот: «вероятность увидеть в самолёте террориста с бомбой мала, а вероятность увидеть двух террористов — вообще мизерна. Потому я беру в самолёт бомбу». Теперь вы понимаете, где кроется ошибка в этом рассуждении и почему вероятность авиационного теракта не уменьшится.
Разновидность: ошибка прокурора
В судебной практике перепутанные вероятности настолько часты, что получили прозвище «ошибка прокурора» = prosecutor’s fallacy: P{гипотеза|улики} ≠ P{улики|гипотеза}.
Известный случай ложного обвинения: Салли Кларк = Sally Clark. У неё в 1996 году умер сначала один ребёнок, потом в 1998 другой. Синдром внезапной детской смертности? 1 к 8500, сразу двое — 1 к 73 млн. Скорее всего, она детоубийца. Её посадили на пожизненное, но она просидела три года. Выяснилось, что второй точно умер от болезни и суд этого не хотел учитывать, но дело не в этом. Цифры 1 к 73 млн тоже были слабые, ведь шансы двойного убийства к шансу двух СВДС — от 1:4,5 до 1:9. Салли так и не оправилась от такого удара.
Другой пример ложного обвинения (People vs Collins, 1968) — свидетели сказали о межрасовой паре (1:1000): блондинка (1:3) с хвостиком (1:10) и негр с бородой (1:10) и усами (1:4), на жёлтой машине (1:10). Поймали похожую пару, эксперт-математик перемножил вероятности и получил 1 к 12 млн, но что это? Вероятность того, что мы возьмём пару из генеральной совокупности, и она будет подходить под описание. Тут дело дошло до верховного суда Калифорнии, и Коллинзы не загремели в тюрьму — условная вероятность, что пара, подходящая под такое описание, невинна, более 40 %. К тому же бородатый, скорее всего, будет с усами, так что множить некорректно.
См. также: Парадокс Спящей красавицы.
Связанные методы: Подмена источника данных, Нерепрезентативная выборка
Разновидность: путать матожидания разных случайных величин
Вернёмся к автобусам, которые плохо ходят. Существует автобусный парадокс: если стоять на остановке с секундомером, видим, что автобусы ходят раз в 10 минут. Правда ли, что среднее ожидание автобуса — 5 минут? Да только в одном случае: ровно каждые десять минут по маршрутной полосе в любую погоду, при любом пассажиропотоке с остановки выходит автобус. Если автобусы ходят случайно, ожидание будет больше: в большой интервал проще попасть. Средний интервал и среднее ожидание — это разные (хоть и связанные) случайные величины, и рассмотрим несколько экстремальных случаев.
- Несколько автобусов особо расхлябанных частников ходят с разных направлений (например, из окрестных микрорайонов — а нам ехать по скоростной сети и не важно, что брать). Получается экспоненциальное распределение, которое, как известно, не имеет последействия — то есть среднее ожидание будет всё те же 10 минут независимо от того, насколько давно был автобус.
- Другое важное достижение из теории массового обслуживания. Пусть человека стригут, например, полчаса. Если ровно каждые 40 минут к парикмахеру приходит человек — у него не будет очередей. Если они приходят всё тем же экспоненциальным потоком — будут очереди, и при стремлении этих условных 40 минут к времени стрижки, 30 минутам, средний простой стремится к бесконечности. Если вернуться к автобусам: всегда нужен запас провозной способности — и на флуктуации пассажиропотока, и на неравномерные интервалы. Это один из признаков хорошего общественного транспорта, хоть и невыгодный для транспортников.
- В попытке саботировать общественный транспорт три автобуса выпускают пачкой. Автобусы, получается, ходят в среднем раз в 10 минут. Но даже если они ходят чётко по расписанию, среднее время ожидания — 15 минут.
Агрегация искажает тенденцию (парадокс Симпсона)
Если в выборках есть перекосы в объёме и условных вероятностях, то при их объединении тенденция может даже смениться на противоположную!
Классический пример — две больницы: районная и специализированная. В специализированной общая смертность больше, потому что туда идут с тяжёлыми случаями. Но любой здравомыслящий человек при прочих равных захочет сделать себе операцию именно в специализированной. Другой вопрос, что прочих равных обычно не бывает: в «крутой» больнице дороже, длиннее очередь, сложнее с транспортом… Но давайте посмотрим на «живые» цифры.
В 1972 году и впоследствии в 1992 в Великобритании прошло исследование по заболеваниям щитовидной железы и сердца у женщин. Нас интересует один кусок этого исследования — смертность пожилых женщин при курении. Было проверено, умерла женщина 20 лет спустя или нет (возраст показан на начало исследования).
| Курит | Нет | |
|---|---|---|
| Умерло | 107 | 132 |
| Выжило | 174 | 175 |
| % умерших | 38,1 % | 43,0 % |
Что, сигарета спасает жизни? Не всё так просто.
| 45…54 | 55…64 | 65…74 | ||||
|---|---|---|---|---|---|---|
| Курит | Нет | Курит | Нет | Курит | Нет | |
| Умерло | 27 | 12 | 51 | 40 | 29 | 101 |
| Выжило | 103 | 66 | 64 | 81 | 7 | 28 |
| % умерших | 20,8 % | 15,4 % | 48,6 % | 33,1 % | 80,6 % | 78,3 % |
В молодом возрасте много курят, а шансы умереть малы. В старости обычно врач или обстоятельства не дают курить, большинство курильщиц перемёрло, и курящая старуха, скорее всего, будет отличаться завидным здоровьем, зато вероятность помереть высока и так.
Если уж нужны именно две цифры — вероятность умереть в том или ином случае — приходится перевзвешивать выборки, чтобы привести их к обычному распределению по возрастам. А так излишняя агрегация данных — зло; если в выборках есть перекосы, надо их высветлять, а не заметать под ковёр агрегации.
Связанные методы: Давать на сравнение совершенно разные цифры; спутать априорную, условную и апостериорную вероятность; проблема Нью-Йорка и Монтаны.
Ошибки с процентами
Например: добавили 25 % и отняли 25 %, и получилось 1,25·0,75 ≈ 0,94. А не единица.
Бывает и такая штука.
— Какие зубные пасты вы рекомендуете?
— Да любые.
— Назовите несколько.
— Ну А, Б, В…
Вот и выходит: «80% стоматологов рекомендуют пасту Б».
Скрыть малую выборку за излишней точностью
Из книги Дарелла Хаффа «Как лгать при помощи статистики»: «Давным-давно, когда Университет Джонса Хопкинса только начал принимать девушек, некто, не испытывавший особых восторгов по поводу совместного обучения, обнародовал данные, ставшие для многих потрясением: оказывается, 33 1/3 % студенток университета повыходили замуж за преподавателей! Однако исходные цифры позволяли точнее оценить картину „бедствия“. На тот момент в списке учащихся числились три девушки-студентки, и одна из них действительно вышла замуж за преподавателя».
В общем, если «да» ответило 4 из 17, надо писать «24 %» или даже «25 %», но не «23,5 %». Как говорят математики, «лишняя цифра — половина ошибки». Поэтому, кстати, манипуляторы не любят круглых выборок: не получается наделать много значащих цифр.
Общее правило здесь — число значащих цифр не должно превышать число цифр в размере выборки (исключая степени десятки, естественно). Так, если в опросе приняло участие 880 человек и 456 из них ответили «да» — то результат деления нужно округлять до третьей цифры, то есть до 51,8 %. Разница между десятыми долями процента — уже больше одного человека, поэтому сотые доли не имеют никакого смысла. Излишнее число знаков позволяет скрыть совпадение или круглое число, которое не нравится манипулятору.
Нечасто используется надпись «24 %»: если последняя цифра точная (±1 единица), она крупная; если её погрешность до 3 единиц (≈√10), её пишут мелко; если ещё выше — цифра опускается.
Умалчивание доверительного интервала
Тесты на IQ сами по себе предвзятые: по мнению Вассермана, они исследуют небольшую часть человеческих способностей, и на них можно натаскаться. Но речь не об этом. Если у одного человека IQ=98, а у другого 101, правда ли, что один умнее другого? Нет, особенно если в полной записи теста написано «98±3» и «101±3».
Однажды провели исследование по содержанию вредных веществ в сигаретах. Одна из марок оказалась на последнем месте с пренебрежимым отрывом — и она по этому поводу устроила рекламную кампанию, какие они маловредные.
Интегральные цифры там, где читатель их не ожидает
Ложная корреляция
Под корреляцией будем подразумевать любую статистически значимую функциональную зависимость; не обязательно классическую линейную или ранговую корреляцию.
Выдавать корреляцию за причину-следствие
Ошибка техасского стрелка бывает и в корреляциях: пересматриваем сотню параметров, находим, что среди них какие-то два коррелируют, и сообщаем: между ними статистически значимая корреляция! Так-то так, но само по себе наличие корреляции ни о чём не говорит. Оно может быть вызвано как действительно наличием причинно-следственной связи (причём в любом направлении!), так и тем, что на оба рассматриваемых параметра влияет какой-то третий или же просто случайным совпадением.
Противники курения по обе стороны железного занавеса любили подчёркивать, что курильщики плохо учатся. И забывают, что возможны, грубо говоря, пять вариантов:
- курят → отстают в развитии (прямая зависимость)
- плохо учатся → закуривают стресс (обратная зависимость). Между прочим, обитатели студенческих общежитий, даже в лучших вузах, очень часто закуривают по сравнению с местными или живущими на квартире.
- неурядицы в семье → курят и плохо учатся (третья причина)
- курят → отстают в развитии → самореализуются в плохих компаниях → курят (порочный круг)
- нет никакой связи, корреляция случайная (ложная корреляция)
Третья причина
Классический для русского читателя пример третьей причины — из книги Петра Маковецкого «Смотри в корень». Журавли летят на юг, когда холодно. Где здесь причина, где следствие?
А нет тут причины, они оба — следствия северного ветра. В северный ветер холодно, и он помогает лететь на юг. Другими словами, значимая корреляция бывает потому, что третий фактор влияет и на то, и на другое.
Второй пример: там, где распространяется COVID, ставят 5G. Общая причина — населённое место: там больше контактов (а значит, быстрее распространяется COVID), и там мобильная связь более востребована.
Случайное совпадение
Когда проверяется одновременно N параметров, то количество возможных корреляций между ними равно N(N−1)/2, то есть при проверке 20 параметров число корреляций составляет 190. Из такого большого количества часть корреляций может оказаться значимыми просто в силу случайности. Сайт [1] содержит примеры значимых и сильных корреляций между явно не связанными между собой явлениями (например, числом людей, утонувших после падения в бассейн и числом фильмов, в которых снялся Николас Кейдж). Вообще, в такой ситуации положено применять специальные поправки на множественность параметров, но на практике это мало кто делает.
Надо признать, в некоторых случаях на том сайте есть подозрение на третью причину, но без полного набора проверенных данных это сложно установить. Выручка залов игровых автоматов и докторские степени по информатике — общей причиной может быть определённый этап развития компьютеров, в таком случае эти цифры должны разойтись в середине 2010-х, когда модной темой стали нейросети. Импорт нефти и потребление курятины — общей причиной будет экономическое состояние США, при этом потребление курятины должно быть более сглаженным, ведь курятина может вести себя и как как малоценный товар, и как ценный, но труднозаменимый. Продажи японских автомобилей и самоубийства намеренным ДТП — общей причиной может быть доступность автомобиля.
Отсутствуют поправки на покупательную способность валюты
К сожалению, покупательная способность валют стран СССР не так стабильна, как хотелось бы. Курс постоянно растёт, и чтобы сравнивать растущую пенсию даже в пределах нескольких лет, надо делать поправки на инфляцию.
В США тоже есть инфляция, и поправки на неё обязательны, когда счёт идёт на десятилетия.
Передаточному звену выставить источник на посмешище
Многие из нас могут сложить в уме два числа, а некоторые — знакомы с приёмами манипуляции данными. Задача проста: делаем наглую манипуляцию данными, чтобы внимательный мог всё же увидеть, что цифры нечистые. В результате неверной обработки данных будет подорвано доверие к их источнику.
Тут примером будут печально известные «146 %». Не будем выяснять, было это намеренно или просто ошибка в нехитрой программе, готовившей график, главное: ЦИК РФ был выставлен на посмешище.
Разновидность: реальные артефакты в данных объявить манипуляцией
Основная статья: Миф:Гауссиана на выборах
Часто реальные данные не похожи на «идеальные» вероятностные распределения. Например, потому, что генеральная совокупность неоднородная. Или потому, что выборки ограничены и просто статистически ½ и ⅓ выпадают чаще, чем 0,4567.
Манипуляция графиками
Вообще-то, нарисовать график — это тоже обработка. Но весёлые графики — это отдельный жанр креативной статистики.
График без нуля
В биржевой спекуляции с высокими плечами важен рост или падение курса даже на один пункт[1]. Если в анализе временны́х рядов мы слишком далеко ушли от фактического размаха данных — плохой прогноз. Для всего этого графики могут и не иметь нуля.
Но это специфические задачи, и в большинстве задач всё-таки ордината пропорциональна величине. И если тихонько обрезать ось, чтобы 0 ординат был равен, например, тысяче, небольшие колебания будут казаться дикими скачками.
Говорит Дэниел Левитин, автор книги «Путеводитель по лжи».
Если вы отражаете в графике уровень преступности, смертности, рождаемости, дохода — или любое иное количественное множество, которое может принимать нулевое значение,— тогда ноль должен быть минимальной точкой отсчёта. Но если ваша цель — посеять панику или ужас, начните свой график поближе к нижней границе значений, это подчеркнёт разницу, которую вы пытаетесь выделить, потому что ваш глаз привлекает разница, показанная на графике, а настоящий её размер оказывается незамеченным.
Метод крайне частый. Поэтому не забывайте смотреть на шкалу. Если шкала не с нуля, или мелким шрифтом, или график показывают ограниченное время, чтобы шкалу не увидели — вас нажигают! Специфические отрасли, где такой график оправдан, не в счёт.
В столбцовой диаграмме масштаб всегда с нуля. Так что столбцовая диаграмма без нуля — полное нарушение формата, см. ниже.
Разрыв в оси
Достаточно разорвать ось, и далеко отстоящие величины будут казаться близкими.
Трёхмерность
Трёхмерность искажает величины, и этому есть несколько причин.
- Неравномерное искажение (даже в параллельной проекции). Несмотря на то, что параллельная проекция сохраняет площадь фигур, лежащих в одной плоскости, эта самая площадь становится трудночитаемой.
- Искажения, вносимые перспективой. Как собственно перспективные искажения, так и «антиперспективные», когда мы подсознательно исправляем искажения, которых в действительности нет.
- Невозможно совместить штрихи (которые на «стенке» диаграммы) и парящий посередине пузырёк или столбец.
- «Незначимые» части диаграммы — скажем, боковая поверхность цилиндра на секторной диаграмме — увеличивают закрашенную площадь.
- Некоторые кодируют величину объёмом трёхмерной фигуры. Такое вообще не воспринимается на плоском экране — только если покрутить объёмные тела в руках.
А незначительно больше Б, но Б ближе к стенке, и шкала показывает больше.
Здесь незначимая боковая поверхность цилиндра зрительно увеличивает Б.
Перспективные искажения и незначимые поверхности в действии.
Метод крайне частый. Трёхмерные диаграммы иногда хороши, но всю свою силу они проявляют, когда есть возможность их покрутить мышью. А если нет — задумайтесь. Если данные можно успешно показать и в 2D — вас гарантированно дурят!
Более радикальные специалисты (например, Эдвард Тафти, американский статистик, автор нескольких книг по визуализации данных) считают, что секторная диаграмма — в принципе надувательство, так как невозможно сравнить близкие по размеру секторы.
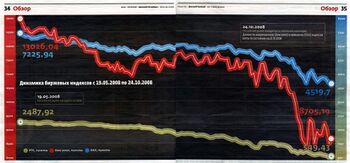
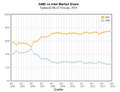
Двойной масштаб
Опять отличились русские СМИ, на сей раз «Деловой Петербург» — роскошно прикрыли ужасающее падение российского биржевого индекса во время кризиса 2008 года.
Оказывается, американский индекс читается по левой шкале, немецкий и русский — по правой. И на обеих шкалах нет нуля.
Действительно, двойной масштаб иногда нужен (например, вывести на один график высоту и скорость самолёта). Но когда данные, которые нужно непосредственно сравнивать, вынесены на разные шкалы — это фол.
Относительные данные рисовать на абсолютной шкале
Хорошо, перерисуем график из «Делового Петербурга» (цифры для простоты взяты не все). Что в нём не так (рис. 1)?
А в том, что биржевой индекс сам по себе никакой роли не играет. Важно, во сколько раз он поднялся или опустился. Если перерисовать график ещё раз, на сей раз в процентах, картина будет удручающая (рис. 2). Стоимость американских акций упала на треть, русских — вчетверо. Спасибо компании Powerlexis и Асе Боярчиковой за красивый пример.
Сходные приёмы: Скрыть тенденцию за мелким масштабом.
Плохо: абсолютная шкала (данные «Деловой Петербург», график компания Powerlexis)
Хорошо: относительная шкала
Фигура, символизирующая величину, растёт по обоим измерениям
Рисуем столбцовую диаграмму. Мелко и некрасиво! Тогда берём и заменяем столбцы на какие-нибудь картинки. Чем больше величина, тем больше картинка. Вот только мозг сразу и не поймёт, что воспринимать: линейные размеры или площадь картинки. (В пузырьковых диаграммах и прочих «законных» применениях этого метода считается, что величина должны быть пропорциональна площади, то есть размер — квадратный корень).
Вариация номер один. Получилось, наоборот, крупно. Чтобы сделать диаграмму компактнее, накладываем одно изображение на другое. Правда, наш мозг отлично исправляет перспективные искажения и тот предмет, который «дальше», кажется больше.
Вариация номер два. Рисуем человечка; размер пропорционален квадратному корню. Для человеческих фигур мы перестаём воспринимать площадь и начинаем воспринимать именно рост.
Метод нередкий. Видишь фигуру, которая растёт по обоим измерениям — будь настороже.
Бывает, что метод оправдан. Например:
- Пузырьковая диаграмма, когда из-за обилия осей приходится подключать и размер пузырька.
- Масштабный чертёж, когда все объекты увеличиваются или уменьшаются в N раз по сравнению с реальностью.
Скрыть важную тенденцию за мелким масштабом
Классический пример (рисунки 1 и 2) — взять колебания среднегодовой температуры океана в пункте A, внести в масштаб 0 °C и сказать: температура меняется незначительно. И человек, привыкший к противоположной манипуляции — преувеличить незначительное растягиванием масштаба — может даже поверить. А ведь изменение температуры даже на градус может привести к немалым экологическим последствиям.
Температура, если она не криогенная, не имеет стандартного нуля, потому в любом случае нужно смотреть на ось.
Другой вариант — показать на одном графике динамику очень большой и очень маленькой величины, и это показано на рисунках 3…5. Рисунок 3 — это настоящая пропаг***онщина: на одном графике сразу некорректный масштаб, вырванные из контекста данные и просто категорическое заявление. Посмотрим на рисунок 4: из-за того, что проверок на рак будет больше, чем абортов, сложно разобраться с динамикой последних. На рисунке 5 крайне редкий и обычной публике пригодный только для масштабов инфляции график — процентное изменение по сравнению с предыдущим годом.
1. Плохо: Ось Y от −23 до 43 °C, размах колебаний 2° (National Review). Внимание, градусы Фаренгейта!
2. Хорошо: График, исправленный интернет-сообществом (Quartz, данные NASA)
3. Ужасно: Зависимость между частотой проверок на рак и абортов (Americans United for Life)
4. Лучше: Те же данные, абсолютные величины (Keith Collins, Politfact, нет данных на 2008)
5. Лучше: Те же данные, процентное изменение год от года (тот же источник)
Скрыть важную тенденцию за неудачным срезом
Самый простой и наглый вариант — метод техасского стрелка. Он относится не к манипуляции графиками, а к манипуляции источниками и там описан подробнее.
Существуют и другие методы.
Логарифмический масштаб там, где зритель не ожидает
Логарифмический масштаб незаменим там, где величина растёт экспоненциально. Он, например, позволяет сравнить, насколько успешно разные страны мира противостоят пандемии коронавируса (2020). Чтобы показать, что масштаб именно логарифмический, можно сделать такое:
- Сделать настолько хорошо видимые подписи к оси, насколько можно.
- Нарисовать линии на 2, 4, 6, 8, 10, 20, 40, 60, 80, 100, 200… Характерный узор, повторяющийся с каждой десяткой, подскажет, что масштаб не линейный.
Если нет ни того, ни другого, зритель может просто не осознать, что масштаб-то логарифмический.
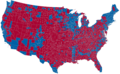
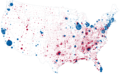
«Проблема Нью-Йорка и Монтаны»
Или, раз уж мы патриоты, Москвы и Сибири. Такое бывает в данных, наложенных на географическую карту: город Нью-Йорк занимает 0,01 % площади США, но содержит 2,7 % населения. Монтана — это 4 % территории и 0,3 % населения. Картинка «Обама против Маккейна» (2008) вся красная, но победил синий Обама. Второй подход также оставляет желать лучшего (сложновато просуммировать площадь этой россыпи, да и цветопередача монитора может вмешаться), но хотя бы ближе к делу.
Плохо: все США красные, но победил синий Обама… (данные реальные, автор графика неизвестен)
Лучше: …и если раскрасить территорию по плотности населения, понятно, почему.
Игра в ассоциации
Roses are red, and violets are blue. Сначала идёт начальная школа, потом среднее образование, потом высшее, потом научное (магистратура, аспирантура, докторантура).
Достаточно спутать цвета или порядок — и график начинает восприниматься намного хуже. В некоторых статистических программах есть предпросмотрщик, позволяющий одним глазком посмотреть на данные, но не дающий настроить график — для подобных выборок, где цвет важен, это бесит!
Метод нередкий, обязательно взгляните на легенду!
Плохо: ведь Intel традиционно синий, AMD — красный или зелёный… (данные собраны программой PassMark Performance Test)
Хорошо: Intel и AMD выкрасили в свои цвета (данных больше, обрываются с дебютом сверхуспешного Ryzen).
Сломанный масштаб
Ещё в шестом классе школьников учат рисовать и читать диаграммы. И то, за что школьнику ставят кол, у взрослых почему-то прокатывает. Сломанный масштаб — вопиющее (и, к сожалению, нередкое) нарушение формата диаграммы.
На первой картинке мы видим производство энергии в США в 1977 году и два прогноза на 2000 (New York Times). Вот только масштаб не соблюдён: почему-то 14>18.
На второй облажалась, как ни прискорбно, RT, сгладив темпы заражения COVID. На график, сделанный телевизионщиками, наложен график, сделанный телезрителем, и видно, что потерян масштаб последних столбцов. Россия не единственная такая — на рис. 3 похожее сделал аргентинский кабельный канал C5N.
1. 14 > 18 (NY Times)
2. Потерян масштаб последних столбцов (RT)
3. Масштаба нет вообще (C5N)
Прочие нарушения формата диаграммы
На первой картинке телеканал Fox Chicago отчитывается о президентских праймериз 2012 года. Чуров отдыхает — в сумме аж 193. Вообще-то цифры хорошие, ведь в опросе разрешалось выбирать несколько ответов. Грех в том, что эти результаты наложили на круговую диаграмму вместо обычной линейной — а ведь зритель предполагает, что полный круг равняется 100 %.
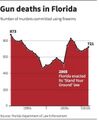
Во многих штатах США есть интересная доктрина: человек может защищать свою собственность вплоть до причинения смерти, и претензий у полиции не возникнет — правда, для этого собственность должна быть размечена, отсюда таблички «Частная собственность», которые мы привыкли видеть в кино. По мнению многих, что-то подобное стоило бы сделать и в России, но дело не в этом. В 2005 году закон приняли и во Флориде, и агентство «Рейтер» разразилось таким графиком (рис. 2). А вы не заметили, что ось ординат растёт вниз и с принятием закона количество смертей от огнестрельного оружия как раз подскочило (рис. 3)?
Четвёртый рисунок сделан из искусственных данных, но не менее показателен: сразу спутанная легенда и непонятного вида трёхмерная фигура.
Пятый пример (пресс-служба Белого дома при Бараке Обаме): в столбцовой диаграмме масштаб всегда с нуля.
1. Целое на круговой диаграмме не 100% (Fox Chicago)
2. Ордината направлена вниз (Reuters)
3. …тот же график, исправленный
4. Конус и спутанная легенда
5. Столбцовая диаграмма без нуля (Белый дом, Барак Обама)
Примечания
- ↑ Биржевой пункт — минимальная единица цены; если цена фиксируется в десятых долях цента, то пункт — 0,1¢. То, что с плечами в 1000 и более обычно торгуют на «форекс-лохотронах» — вопрос другой. Также иногда говорят «процентный пункт» при увеличении, например, с 3 до 4 %.