Манипуляция статистикой

Незавершённая статья Эта статья находится в процессе написания. Сюда следует добавить недостающий материал и устранить проблемы в оформлении и содержании. Вы можете помочь в доработке статьи. Добавьте сюда больше информации.

Манипуляция статистикой — способы заставить ложные данные выглядеть наукообразно и правдоподобно.

Манипуляция источниками данных

Нерепрезентативная выборка

Есть два нарекания к плохим выборкам: маленькая и с перекосами.

Собрать достаточно репрезентативную выборку — это в своём роде искусство, и если оно не прокатывает, может случиться забавное.

Снова-таки, из книги «Как лгать при помощи статистики». Журнал Literary Digest по результатам широчайших (10 млн) опросов пришёл к выводу, что на выборах победит Альфред Лэндон. А победил Франклин Рузвельт. Просто те, кто имели телефон и подписывались на Literary Digest, были достаточно богаты и поддерживали Республиканскую партию.

Другой пример оттуда же. Для испытания прививки от полиомиелита 450 детей привили, 680 оставили. Во время эпидемии ни один привитый не заболел. Здесь вопрос в крайней редкости болезни, в группе такой численности заболеют в среднем двое, и чтобы результат был статистически значим, нужна выборка раз в пятнадцать больше.

Ошибка выжившего

Один из важнейших способов получить выборку с перекосами так, чтобы никто ничего не заподозрил. Когда есть «выжившие», по которым информация легкодоступна, и «погибшие», по которым информации нет, заманчиво взять выборку из «выживших» и сказать: вот репрезентативная выборка. Но это неверно: важная информация скрывается среди «погибших», и хотелось бы восстановить, какая именно. Особенно если задача — не стать «погибшим».

Начнём с примера, который ввёл в обиход математиков ошибку выжившего. Абрахам Вальд, работая математиком на силы Коалиции во Второй мировой войне, получил задачу. Не все бомбардировщики возвращались с полётов. Те, которые всё-таки вернулись, оказались изрешечены пробоинами. Все пробоины нанесли на одну модель; крылья и хвост оказались все в пробоинах, а кабина и центроплан — чистые. Верно ли, что надо добавить брони на крылья и хвост? Вальд сказал: нет! Они все в пробоинах, потому что достаточно прочны. Самолёт, которому попали в кабину, не вернётся, которому попали в крыло — долетит. Потому укреплять надо как раз чистые зоны.

Точно так же из старых машин и зданий дошли наиболее прочные и практичные, рекламист Гельмут Крон («Фольксваген») сыграл на этом: «Теперь таких не делают».

«Погибших» можно делать и искусственно, этим грешат реалити-шоу, которые выводят наименее перспективных участников, пока те не заполучили своих поклонников.

Метод техасского стрелка

Метод техасского стрелка: стрельнуть и нарисовать мишень там, куда стрельнул, а неудачные пробоины залатать. Это связано с другим методом демагогии: Свиногогия.

Из книги Дарелла Хаффа «Как лгать при помощи статистики»: «Предположим, некая немногочисленная группа потребителей в течение полугода ведет учет состояния своих зубов, а потом переключается на пасту от Doakes. Далее можно ожидать одного из трех вариантов: кариеса станет больше, кариеса станет ощутимо меньше или никаких изменений не последует. Если события пойдут по первому или последнему варианту, производитель пасты просто зафиксирует эти показатели (где-нибудь у себя, вдали от глаз общественности) и предпримет новые попытки. Рано или поздно в дело вмешается случай, и у испытуемых зафиксируют-таки значительное улучшение, достойное газетных заголовков, а то и целой рекламной кампании. И случится это независимо от того, пользуются ли испытуемые пастой Doakes, питьевой содой или своим привычным средством по уходу за зубами».

Давать на сравнение совершенно разные цифры

Известный рекламный трюк: подключить второй фактор и сделать вид, что он ни к чему. Из статьи Сергея Абдульманова «Как айтишник по магазинам ходил»:

А вот про такое я даже не думал. Давайте ещё раз: они обещают мне заметный результат через две недели. Как они проверили? Мыли голову вот этой штукой и, внимание, фокус, ещё одной другой штукой. И эти обе штуки вместе оказали заметный результат. Почти идеальная логика.

Из книги Дарелла Хаффа «Как лгать при помощи статистики»:

В Америке псевдообоснованные цифры переживают бум раз в четыре года. Впрочем, это не свидетельствует о циклической природе таких цифр, а просто напоминает, что именно с такой периодичностью проходят выборы. Предвыборное заявление, обнародованное Республиканской партией в октябре 1948 г., целиком и полностью построено на цифрах. Создается видимость, что эти цифры связаны друг с другом, но это не так:

Когда Дьюи в 1942 г. был избран на пост губернатора, минимальный размер зарплаты учителей в некоторых районах составлял такую малость, как $900 в год. Сегодня школьные учителя в штате Нью-Йорк получают самые высокие зарплаты в мире. По рекомендации губернатора Дьюи, которая основывалась на сведениях, полученных в ходе работы назначенного им комитета, легислатура штата выделила из бюджета штата $32 000 000 на обеспечение немедленного повышения заработной платы школьным учителям. В результате минимальный размер зарплаты учителя в Нью-Йорке варьируется в пределах от $2500 до $5325.

Совершенно не исключено, что мистер Дьюи проявил себя как друг учителей, да только приведенные цифры об этом не свидетельствуют. Это старый как мир трюк с «было» и «стало», когда для показа разительных перемен втихомолку приводят в действие ряд факторов, а потом представляют дело так, будто эти факторы ни при чем. Здесь у нас имеется «было» $900 и «стало» от $2500 до $5325. Это, бесспорно, создает впечатление, что положение улучшилось. Но меньшая цифра отражает нижний порог зарплаты учителя в каком-нибудь сельском районе штата, а цифры побольше — диапазон заработных плат учителей в самом Нью-Йорке. Может быть, при губернаторе Дьюи улучшения действительно произошли, а может быть, и нет.

Оттуда же:

Ещё один образчик подмены объекта исследования явил сенатор Уильям Лангер, когда возопил, что «мы могли бы взять заключенного из „Алькатраса“ и поместить на содержание в „Уолдорф-Асторию“ — дешевле бы обошлось…» Дело в том, что сенатор от Северной Дакоты ссылался на ранее опубликованные данные, что содержать узника в тюрьме «Алькатрас» стоит $8 в сутки, а «это стоимость номера в хорошем сан-францисском отеле». Здесь произошла подмена общих затрат на содержание (в «Алькатрасе») на одну только стоимость номера в отеле.

Подмена источника данных

Как говорят, «по результатам опроса, проведённого в Интернете, 100 % населения подключены к интернету».

Более тонкая манипуляция: скажи возраст жены. На 35 годах будет пик, выше, чем 34 или 36 — просто потому, что если кто-то возраст не помнит, даёт округлённую цифру.

Манипуляция обработкой

Спутать среднее, медиану, моду и квантиль достаточного уровня

Начнём с неформальных определений.

• Математическое ожидание случайной величины — это, грубо говоря, «среднее по бесконечной выборке».
• Мода — наиболее часто встречающееся значение.
• Квантиль уровня α — такой x, что вероятность попасть в диапазон (−∞; x) будет α, а в диапазон [x; +∞) — соотвественно, 1−α. Слово «квантиль» мужского рода.
  • Квантиль уровня 0,5 — вероятность «недолёта» 0,5 и вероятность «перелёта» 0,5 — называется медианой.
  • Три квантиля уровней 0,25, 0,5 и 0,75 — квартили. Девять квантилей уровней с 0,1 по 0,9 — децили. 99 квантилей с 0,01 по 0,99 — процентили.

У нас в статистике, к сожалению, нет математически заданной случайной величины, есть только выборки. Что с ними можно сделать?

• Математическое ожидание можно приблизить выборочным средним.
• Чтобы найти моду, строят гистограмму, сглаживают её, убирая случайные колебания, и её максимум будет модой. Несколько максимумов — несколько мод.
• Чтобы найти медиану, выстраивают экспериментальные значения по порядку и берут центральный. Точно также — при достаточном размере выборки — можно получить любой квантиль.

Когда распределение симметричное и колоколообразное, матожидание, медиана и мода совпадают. Но часто статистика имеет дело с несимметричными распределениями. Так, если в фирме босс, получающий 10000 $, два инженера с доходом 1500, пять токарей с доходом 800 и семь грузчиков с доходом 300, имеем среднее 1273 $, медиану 800 и моду 300. Выбирай любое среднее в зависимости от того, в каком свете хочешь показать доходы.

Другое заблуждение более хитрое — и, к сожалению, очень распространённое. Берём медиану или среднее, и считаем, что эта цифра — надёжная граница. Живой пример.

Не все из нас живут под метро, а автобусы обычно ходят случайно и с неприемлемо долгими интервалами. Допустим, поездка «в среднем» длится 45 минут. Подсознательно хочется выходить за 45 минут до времени Ч, особенно сильным мужчинам, которые могут бегом подсократить пешеходное плечо. Но слишком уж часто приходится бежать: если ваше «среднее» — это медиана, в половине случаев вы будете опаздывать; если это среднее арифметическое — несколько реже. Успевать при любых обстоятельствах? Непрактично, особенно если закладываться на такие редкие события, как забастовку транспортников или теракт. Потому надо говорить: нас, например, устраивает успевать на 90 % встреч. Другими словами, нужный срок выхода — квантиль уровня 0,9.

Из книга Дарелла Хаффа «Как лгать при помощи статистики»: «Сходным образом мелкие опущенные детали в труде под названием „Нормы развития Гезелла“ ввергли в панику папочек и мамочек. Дай только родителю прочитать раздел, где говорится, что в возрасте стольких-то месяцев ребенку уже полагается сидеть, и он сейчас же примерит это к собственному малышу. А поскольку примерно половина детей к указанному возрасту всё ещё не научилась сидеть, это сделало несчастными многих и многих родителей. Этого недоразумения во многом удалось бы избежать, если бы наряду с показателем „нормы“ или среднего значения был бы указан диапазон этой самой нормы. Тогда родители увидели бы, что их дети попадают в пределы нормы и прекратили бы беспокоиться по поводу мелких и ничего не значащих отклонений».

Спутать априорную, условную и апостериорную вероятность

Допустим, мы исследуем вероятность заболеть, если был привит и если не был. Тогда у нас:

• Априорная вероятность — вероятность заболеть (уколот ли — неизвестно).
• Условная вероятность — вероятность заболеть, если был привит. Или если не был.
• Апостериорная вероятность — вероятность, что ты привит, если ты заболел (или если не заболел).

Априорная вероятность связана с условными по формуле полной вероятности. Апостериорная вероятность связана с условными по формуле Байеса.

Например (цифры выдуманные): из 100 уколотых заболели 20. Из 10 отказавшихся заболели все. Тогда:

• Априорная вероятность — 30/110 ≈ 0,27.
• Условная вероятность, если привит — 0,2. Условная вероятность, если не привит — 1.
• Апостериорная вероятность быть привитым, если не заболел — 1. Если заболел — 20/30 ≈ 0,67.

Вот мы смотрим на последнюю цифру и говорим: двое из трёх заболевших привиты! А ведь прививка превращает почти верную болезнь в 20 %!

Из книги Дарелла Хаффа «Как лгать при помощи статистики»: «Уровень смертности в военно-морском флоте США в период Испано-Американской войны 1898 г. составлял девять человек на тысячу. За тот же период уровень смертности среди гражданского населения Нью-Йорка достигал шестнадцати человек на тысячу. Позже эти цифры использовали вербовщики, чтобы показать: служить в ВМС безопаснее, чем находиться за его пределами. Допустим, что сами эти цифры точны (вероятно, так оно и есть). Давайте остановимся на мгновение и проверим, сообразите ли вы, что лишает практически всякого смысла сами эти цифры, или хотя бы заключение, которое выводили из них вербовщики. Всё дело в том, что группы, к которым относятся вышеуказанные цифры, несопоставимы. В рядах ВМС служат главным образом молодые мужчины, признанные здоровыми. Гражданское же население состоит среди прочего из малых детей, стариков и больных, и для этих категорий населения уровень смертности выше, где бы они ни находились».

На языке математики: одну условную вероятность (вероятность умереть на гражданке, если ты не годен в армию) выдаём за другую (вероятность умереть на гражданке, если ты годен).

См. также: Парадокс Спящей красавицы.

Связанные методы: Подмена источника данных, Нерепрезентативная выборка

Передаточному звену выставить источник на посмешище

Набившие всем оскомину 146 %

Многие из нас могут сложить в уме два числа, а некоторые — знакомы с этими приёмами. Задача проста: делаем наглую манипуляцию данными, чтобы внимательный мог всё же увидеть, что цифры нечистые. В результате неверной обработки данных будет подорвано доверие к их источнику.

Тут примером будут печально известные «146 %». Не будем выяснять, было это намеренно или просто ошибка в нехитрой программе, готовившей график, главное: ЦИК РФ был выставлен на посмешище.

Скрыть малую выборку за излишней точностью

Из книги Дарелла Хаффа «Как лгать при помощи статистики»: «Давным-давно, когда Университет Джонса Хопкинса только начал принимать девушек, некто, не испытывавший особых восторгов по поводу совместного обучения, обнародовал данные, ставшие для многих потрясением: оказывается, 33 1/3 % студенток университета повыходили замуж за преподавателей! Однако исходные цифры позволяли точнее оценить картину „бедствия“. На тот момент в списке учащихся числились три девушки-студентки, и одна из них действительно вышла замуж за преподавателя».

В общем, если «да» ответило 4 из 17, надо писать «24 %» или даже «25 %», но не «23,5 %». Как говорят математики, «лишняя цифра — половина ошибки». Поэтому, кстати, манипуляторы не любят круглых выборок: не получается наделать много значащих цифр.

Манипуляция графиками

Вообще-то, нарисовать график — это тоже обработка. Но весёлые графики — это отдельный жанр креативной статистики.

График без нуля

Что будет, если исключить 0 из шкалы

В биржевой спекуляции с высокими плечами важен рост или падение курса даже на один пункт. Если в анализе временны́х рядов мы слишком далеко ушли от фактического размаха данных — плохой прогноз. Для всего этого графики могут и не иметь нуля.

Но это специфические задачи, и в большинстве задач всё-таки ордината пропорциональна величине. И если тихонько обрезать ось, чтобы 0 ординат был равен, например, тысяче, небольшие колебания будут казаться дикими скачками.

Метод крайне частый. Поэтому не забывайте смотреть на шкалу. Если шкала не с нуля, или мелким шрифтом, или график показывают ограниченное время, чтобы шкалу не увидели — вас нажигают! Специфические отрасли, где такой график оправдан, не в счёт.

Двойной масштаб

Падение биржевых рейтингов по версии «Делового Петербурга»

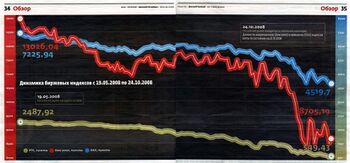
Опять отличились русские СМИ, на сей раз «Деловой Петербург» — роскошно прикрыли ужасающее падение российского биржевого индекса во время кризиса 2008 года.

Оказывается, американский индекс читается по левой шкале, немецкий и русский — по правой. И на обеих шкалах нет нуля.

Действительно, двойной масштаб иногда нужен (например, вывести на один график высоту и скорость самолёта). Но когда данные, которые нужно непосредственно сравнивать, вынесены на разные шкалы — это фол.

Относительные данные рисовать на абсолютной шкале

Перерисованный график (абсолютная шкала)

Перерисованный график (относительная шкала)

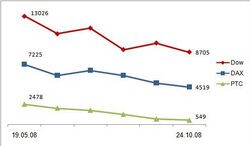
Хорошо, перерисуем график из «Делового Петербурга» (цифры для простоты взяты не все). Что в нём не так (рис. 1)?

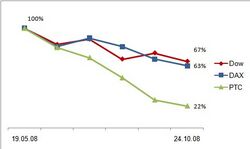
А в том, что биржевой индекс сам по себе никакой роли не играет. Важно, во сколько раз он поднялся или опустился. Если перерисовать график ещё раз, на сей раз в процентах, картина будет удручающая (рис. 2). Стоимость американских акций упала на треть, русских — вчетверо. Спасибо компании Powerlexis и Асе Боярчиковой за красивый пример.

Сходные приёмы: Скрыть тенденцию за мелким масштабом.

Масштаб определяется не закрашенной площадью, а чем-то другим

Существует забавная вариация этого метода. Рисуем человечка; масштаб пропорционален квадратному корню. Для человеческих фигур мы перестаём воспринимать площадь и начинаем воспринимать именно рост.

Метод нередкий. Иногда он бывает оправдан (т. н. пузырьковая диаграмма), но всё-таки: видишь фигуру, которая растёт по обоим измерениям — будь настороже. Если эта фигура — не круг и не квадрат, вас гарантированно дурят! Сравнение разных предметов в масштабе, разумеется, не в счёт.

Начхать на все договорённости

Ещё в шестом классе школьников учат рисовать и читать диаграммы. И то, за что школьнику ставят кол, у взрослых почему-то прокатывает.

На первой картинке мы видим производство энергии в США в 1977 году и два прогноза на 2000 (New York Times). Вот только масштаб не соблюдён: почему-то 14>18.

На второй — телеканал Fox Chicago отчитывается о президентских праймериз 2012 года. Чуров отдыхает — в сумме аж 193. Вообще-то, цифры хорошие, ведь в опросе разрешалось выбирать несколько ответов. Грех в том, что эти результаты наложили на круговую диаграмму вместо обычной линейной — а ведь зритель предполагает, что полный круг равняется 100 %.

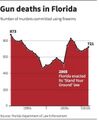
Во многих штатах США есть интересная доктрина: человек может защищать свою собственность вплоть до убийства, и претензий у полиции не возникнет — правда, для этого собственность должна быть размечена, отсюда таблички «Частная собственность», которые мы привыкли видеть в кино. По мнению многих, что-то подобное стоило бы сделать и в России, но дело не в этом. В 2005 году закон приняли и во Флориде, и агентство «Рейтер» разразилось таким графиком (рис. 3). А вы не заметили, что ось ординат растёт вниз и с принятием закона количество огнестрельных убийств как раз подскочило (рис. 4)?

• 

  График без масштаба

• 

  Целое на круговой диаграмме не 100%

• 

  Ордината направлена вниз

• 

  Исправленный график