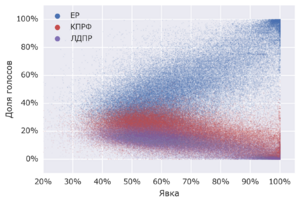
Миф:Гауссиана на выборах

Материал из Русского эксперта
Перейти к навигации Перейти к поиску
Распределение числа поданных голосов по явке участках, выборы в Госдуму 2016 (Источник). Авторами графика предпринята попытка выделить «дополнительные» относительно условной гауссианы голоса за «Единую Россию».

Вскоре после выборов в Госдуму 4 декабря 2011 гг. оппозиционными кругами был раскручен миф о том, что якобы о массовых фальсификациях на выборах свидетельствуют отклонения распределения числа голосов по явке на избирательных участках от кривой Гаусса (гауссиана — нормальное, или Гауссово распределение вероятностей). Последователи этого мифа утверждают, что отклонения от нормального распределения возникают из-за вбросов, каруселей и подлогов итоговых данных.

Данный тезис широко использовался сторонниками белоленточного движения, которые пытались с помощью теории о массовых фальсификация дискредитировать победу партии «Единая Россия» на выборах в Госдуму 2011 года, а также оправдать полнейшее поражение либеральных партий на тех же выборах. После ещё более провальных для оппозиции выборов в Госдуму 2016 года имели место отдельные попытки возродить миф о гауссиане, хотя он был давным-давно разобран и разоблачён.[1]

Опровергается миф элементарно: распределение голосов на выборах не является случайной величиной и вовсе не обязано иметь иметь вид «гауссова колокола». На многих выборах во многих странах распределение голосов за отдельные партии сильно отличается от гауссова распределения, и это совершенно нормально. Чем менее однородна страна по социальному составу и по особенностям голосования избирателей на разных участках, тем более вероятность появления значительных отклонений от случайного распределения. В том числе и Россия не является электорально однородной страной: на большинстве сельских избирательных участков (особенно в отдельных национальных республиках), а также на малых внегородских и внесельских участках (например, в воинских частях) с высокой явкой голосуют преимущественно за партию власти, что и объясняет внешний вид графиков распределения голосов по явке.

Ещё один ложный аргумент, связанный с распределением избирательных участков по долям голосов, поданных за отдельные партии — это так называемая «гребёнка Чурова» («борода Чурова») — хорошо видные на графике небольшие пики, возникающие на числах процентов, кратных 5. По мнению сторонников теории фальсификации, эти «красивые» доли возникают искусственно, в ходе подтасовок. В действительности же, «гребёнка Чурова» — это естественным образом возникающий статистический артефакт: просто таких «красивых» долей и, соответственно, пиков на графике, чисто математически всегда больше, чем других долей, а при значительном числе избирательных участков с малой численностью избирателей — ещё больше.

Возникновение мифа

В декабре 2011 года появилось несколько публикаций и интервью физика Сергея Шпилькина, в которых он заявил, что «Единая Россия» получила якобы аномальное число голосов на избирательных участках с высокой явкой, а кривая распределения голосов для «Единой России» вместо «гауссова колокола» (с одним главным пиком) приняла форму с двумя пиками — в середине и в конце распределения. [2][3] О том же самом Шпилькин заявил и в 2016 году. [4]

Распределение доли голосов по явке (отдельные участки), выборы в Госдуму 2011. Видна следующая корреляция: чем больше явка, тем больше голосов за Единую Россию.

По мнению Шпилькина и подхвативших этот тезис белоленточников и просто недалёких публицистов, такие отклонения от гауссианы свидетельствуют о фальсификации выборов в пользу «Единой России». По форме кривой общего распределения голосов Шпилькин «определил», что не менее 45 % голосов за «Единую Россию» были сфальсифицированы. [5]

Разбор мифа

Несостоятельность гипотезы об обязательности гауссианы

Для начала: рассматриваемые здесь процессы (распределение голосов на выборах) в статистике описываются вовсе не нормальным, а так называемым логнормальным распределением — оно отличается от нормального длинным «хвостом», то есть оно заведомо несимметрично. [6]

Далее, основы мифа применительно к выборам разбирает математик Сергей Кузнецов:

Шаманы говорят: «Cмотри, народ, в любых случайных процессах наблюдается Гаусс! Хочешь пульки в мишень стреляй, хочешь одноклассников по росту измеряй — везде Гаусс! Одно только распределение голосов за Единую Россию, да явка на выборы в ГосДуму — горбатые монстры с диавольским хвостом!»

Но дело в том, что люди — не пульки, и голосуют они не случайным образом, и голоса их по избирательным участкам распределены ну никак не независимо.

Представьте себе, что в 1760 году в Северной Америке устраивают президентские выборы. Две кандидатуры — Чингачгук Большой Змей и Георг II. Кто-то усомнится в том, что График А для таких голосований будет, мягко говоря, не похож на гаусса? УИК’и, находящиеся в вигвамах, очевидно, покажут 100% за первого кандидата и 0% за второго, а УИК’и в городских мэриях — строго наоборот.

...

При этом, чем больше неоднородность страны, тем больше шансов, что итоговая кривая будет иметь «неправильную» форму. А в условиях кризиса, который по-разному сказался на различных группах населения, рост поляризации мнений ещё более вероятен. Отсюда большая, по сравнению с некоторыми предыдущими выборами, неоднородность графика. [7]

В качестве дополнения отметим, что помимо неслучайности голосования и неоднородности распределения избирателей и избирательных предпочтений по участкам, важным аргументом против теории массовых фальсификаций является невозможность централизованно организовать массовые вбросы без угрозы немедленного разоблачения. Действительно, довольно абсурдно представление о некоем всероссийском заговоре, в котором должно участвовать порядка 100 тысяч дисциплинированных заговорщиков, которые массово вбрасывают порядка десяти и более миллионов бюллютеней, при этом ещё порядка миллиона человек в общей сложности всё это считает, контролирует, наблюдает — и в итоге почему-то никто не проговаривается о массовых скоординированных сверху вбросах, а зафиксированное наблюдателями общее число нарушений оказываются на вполне нормальном уровне для страны, где более сотни миллионов избирателей и потому всегда будут происходить отдельные эксцессы.

Причины статистических «аномалий» на выборах в России

Зависимость количества УИК, разделенных по принципу город-село от явки избирателей (по 25 регионам Европейской РФ). Видно, что на сельских избирательных участках явка гораздо выше (в среднем более 80 %), чем на городских участках. Источник.

Подробный разбор статистических «аномалий» на российских выборах был опубликован ещё в 2008 году. В числе авторов разбора — тогдашний глава Центризбиркома Владимир Чуров, которого белоленточники потом обвиняли в фальсификациях, ссылаясь на эти самые «аномалии». Характерно также, что привлечение внимания широкой публики к этим «аномалиям» состоялось не в том же 2008 году, а лишь в 2011 году, что указывает на скоординированный характер информационной атаки на российскую власть в ходе попытки белоленточной цветной революции.

Вот что пишет Чуров с соавторами по результатам исследования 25 регионов Европейской России (см. также график справа):

В селах, где взаимосвязи между людьми гораздо прочнее и глубже, чем в городе, гораздо выше средняя явка и однороднее предпочтения. В городах, где эти связи слабые, явка ниже и предпочтения изменяются от региона к региону, что говорит о большей неоднородности самого массива городов, по отношению к селам.
Что касается судовых, закрытых и иных УИК, то тут, хотя вклад их по голосам незначителен, однородность достаточно большая (около половины имеют явку 100%).

Именно на многочисленные сельские избирательные участки с высокой явкой и однородными избирательными предпочтениями приходится значительная часть голосов за «Единую Россию» — на графике распределения голосов по явке это видно как широкий хвост или даже пик кривой ближе к высоким значениям явки. Кстати, небольшой подъём на высоких значениях явки виден и для партии КПРФ — второй по популярности на селе.

Почему село массово голосует за партию власти? Отчасти, потому, что сельское хозяйство России находится на мощном подъёме, и по сравнению с 1990-ми годами жизнь в большинстве российских сёл и деревень заметно улучшилась. Отчасти также потому, что сельский избиратель более консервативен, прагматичен и гораздо хуже знаком со всеми прочими политическими партиями, кроме «Единой России» и КПРФ: до сельской глубинки агитаторы остальных партий просто не доезжают, а их предвыборные программы расчитаны больше на городских жителей и на селе не актуальны.

Также стоит учесть, что значительная часть сельского населения (да и городского тоже) проживает в национальных республиках и едва ли будет голосовать за альтернативные партии в силу их идеологии и лозунгов (националисты сразу отметаются, либералы противопоставляют «просвещенный Запад» российской «азиатчине», коммунисты непопулярны в связи с религиозными гонениями и депортациями народов во времена СССР) — поэтому остаётся только партия власти.

Наконец, небольшая, но всё же важная часть избирателей (около 1 %), голосуют на внегородских и внесельских участках с явкой, близкой к 100 % (военные части, суда в море и т. д.). По очевидным причинам «Единая Россия» имеет преимущество на большинстве таких участков по сравнению с другими партиями. Впрочем, значительная часть военных, моряков, нефтяников и газовиков голосует на обычных городских участках, и у всех этих сравнительно дисциплинированных профессиональных групп есть серьёзные основания регулярно, от выборов к выборам, голосовать за Путина и «Единую Россию».

Подмиф: «гребёнка Чурова»

Распределение числа УИК по доле голосов за партию («гребёнка Чурова»)
Детальный график распределения числа УИК по доле голосов за партию, выборы 2011 года. Источник.

Идиомами «гребёнка Чурова» или «борода Чурова» (в честь тогдашнего главы Центризбиркома РФ Владимира Чурова) сторонники теории массовых фальсификаций окрестили график распределения количества УИК по проценту поданных за партию голосов (см. график справа), на котором видны пики на «круглых» (кратных 10 и 5) значениях долей. По мнению сторонников теории массовых фальсификаций, эти пики являются доказательством подтасовок на выборах — якобы на отдельных участках для «Единой России» специально рисовали красивые круглые цифры якобы поданных голосов.

Разбор «гребёнки»

Сразу можно отметить, что такие же пики присутствуют: на аналогичных графиках по выборам в других странах, включая «оплоты демократии», и такие же пики, хоть и менее выраженные, видны для оппозиционных партий, например КПРФ.[8]

Причины же данного феномена легко назовёт любой компетентный математик.

  • Во-первых, чисто математически одни доли (дроби вида n/m, где n < m) встречаются чаще, чем другие (рассматривается ограниченная сверху по значению m выборка). Вновь предоставим слово Сергею Кузнецову:
В районе 50% обязан быть скачок, обусловленный тем, что дробь 1/2 среди других дробей n/m встречается чаще остальных. Но этот скачок легко сгладить, взяв слишком широкий шаг диаграммы. То же самое относится и к другим «красивым» дробям — 1/3, 2/3, 3/4, 4/5 и т.д. Чем «красивее» дробь, тем более резким в её окрестности будет пик. [9]
Всё это хорошо видно, если посмотреть на настоящий график распределения числа участков по проценту голосов, без сглаживания и просчитанный с высокой детализацией (см. справа).
Таким образом, избирательных участков, на которых за ту или иную партию проголосовала какая-то «красивая» («круглая») доля избирателей, всегда будет несколько больше, чем иных участков.
  • Во-вторых, значительное число реальных избирательных участков — это малые участки, на которых может быть зарегистрировано всего лишь десять-двадцать человек. В таких условиях вероятность появления «красивых» долей еще больше возрастает: скажем, на многих участках за одну и ту же партию могло проголосовать 9 человек из 10 имеющихся избирателей, или 7 из 10, 19 из 20 и т. д.
При этом именно «Единая Россия», как было указано выше, имеет особую популярность на малых участках (сельских, военных и т. д.), поэтому на графике для этой партии на «красивых» и при этом больших долях будут особенно ярко выражены пики.

«Статические аномалии» в других странах

Исследования выборов в Германии, США, Польше, Израиле и Великобритании показывают, что и там наблюдаются ровно те же «статические аномалии», что и на выборах в России:

Особенно яркий пример: на президентских выборах США 2008 года в штатах Нью-Йорк и Мичиган и в округе Колумбия не только на множестве избирательных участков 99 % проголосовали за Обаму, но, более того, абсолютный максимум распределения приходится на 99 %.[10]

Следовательно, или в названных демократических странах «злочинна влада» вбрасывает фальшивые бюллетени миллионами, или же приходится признать, что гауссиана — совершенно негодный для поиска фальсификаций инструмент.

См. также

Ссылки


Источник — http:///index.php?title=Миф:Гауссиана_на_выборах&oldid=144551